In the fascinating realm of mathematics, the study of shapes forms a fundamental cornerstone. Chapter 5 of NCERT Solutions for Class 6 Maths, titled ‘Understanding Elementary Shapes,’ invites students on an illuminating journey into the captivating world of geometric forms and their properties. This chapter is a gateway to comprehending the basic principles of shapes, angles, and lines, which are essential not only in mathematics but also in everyday life.
Our meticulously crafted solutions provide a comprehensive guide to mastering the intricacies of elementary shapes, enabling students to solve problems and explore the geometric wonders that surround us. Dive into this enriching chapter, where the study of shapes unveils a world of order, symmetry, and mathematical beauty, empowering young minds to grasp the language of geometry with confidence.
NCERT Solution for Class 6 Maths Chapter 5 offers a precise and accurate solution to the questions from this particular chapter. Studying it alongside the textbook will help students to improve their preparations, and score higher in their final exam.
Access NCERT solutions for Class 6 Maths Chapter 5 – Understanding Elementary Shapes
Exercise 5.1
1. What is the disadvantage in comparing line segments by mere observation?
Ans: One of the main disadvantage in comparing the line segments by mere observation is that there will be high chances of miscalculation.
2. Why is it better to use a divider than a ruler, while measuring the length of a line segment?
Ans: We know that rulers are very thick. Hence, when we will measure the length, then we can misread the readings due to the thickness. Therefore, it is better to use a divider than a ruler.
3. Draw any line segment, say
AB��
. Take any point
C�
lying in between
A�
and
B�
. Measure the lengths of
AB��
,
BC��
and
AC��
. Is
AB=AC+BC��=��+��
?
Ans: When we will draw any line segment AB=7cm��=7�� where C� is a point lying between A� and B� as shown in the figure below –

We have AC=3cm��=3�� and
BC=4cm��=4��.
Therefore, AB=AC+BC��=��+��
⇒AB=3+4⇒��=3+4
⇒AB=7cm⇒��=7��.
Yes, AB=AC+BC��=��+��.
4. If
A, B, C�, �, C
are three points on a line such that
AB=5cm��=5��
,
BC=3cm��=3��
and
AC=8cm��=8��
, which one of them lies between the other two?
Ans: As, the sum of AB�� and BC�� is equal to the length of the line segment
AC��
. i.e., AC=AB+BC��=��+��
⇒8=5+3⇒8=5+3.
Therefore, the point B� lies in between the line segment
AC��
.
5. Verify whether
D�
is the mid-point of
AG¯¯¯¯¯¯¯¯��¯
.
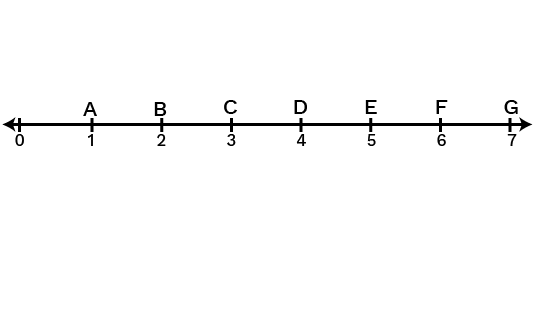
Ans: From the figure we can observe that AD=3cm��=3�� and
DG=3cm��=3��. Therefore, D� is the mid-point.
6. If
B�
is the mid-point of
AC��
and
C�
is the mid-point of
BD��
, where
A�
,
B�
,
C�
,
D�
lie on a straight line, say why
AB=CD��=��
?
Ans:

As, given we have B� is the midpoint of AC��.
⇒AB=BC⇒��=��
Similarly, C� is the midpoint of BD��.
⇒BC=CD⇒��=��
From, the above conditions, we have ⇒AB=CD⇒��=��. Hence, proved.
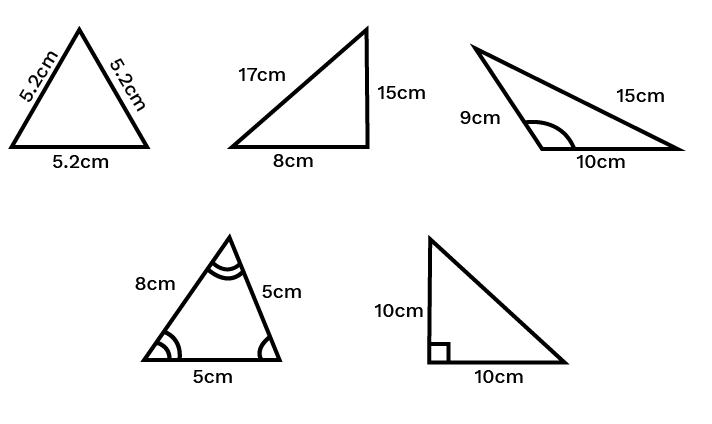
7. Draw five triangles and measure their sides. Check in each case, of the sum of the lengths of any two sides is always less than the third side.
Ans: No, from the given figures below we can conclude that the sum of two sides of a triangle can never be less than the third side of that triangle.
Exercise 5.2
1. What fraction of a clockwise revolution does the hour hand of a clock turn through,
(i) when it goes from
33
to
99
.
Ans: When the hour hand of a clock goes from 33 to 99, the number of divisions between them will be 66, so the fraction will be 612=12612=12.
(ii) when it goes from
44
to
77
.
Ans: When the hour hand of a clock goes from 44 to 77, the number of divisions between them will be 33, so the fraction will be 312=14312=14.
(iii) when it goes from
77
to
1010
.
Ans: When the hour hand of a clock goes from 77 to 1010, the number of divisions between them will be 33, so the fraction will be 312=14312=14.
(iv) when it goes from
1212
to
99
.
Ans: When the hour hand of a clock goes from 1212 to 99, the number of divisions between them will be 99, so the fraction will be 912=34912=34.
(v) when it goes from
11
to
1010
.
Ans: When the hour hand of a clock goes from 11 to 1010, the number of divisions between them will be 99, so the fraction will be 912=34912=34.
(vi) when it goes from
66
to
33
.
Ans: When the hour hand of a clock goes from 66 to 33, the number of divisions between them will be 99, so the fraction will be 912=34912=34.
2. Where will the hand of a clock stop if it:
(a) starts at
1212
and make
1212
of a revolution, clockwise?
Ans: When the hand of a clock starts at 1212 and make 1212 of a revolution, clockwise then it will stop at 122=6122=6.
(b) starts at
22
and makes
1212
of a revolution, clockwise?
Ans: When the hand of a clock starts at 22 and make 1212 of a revolution, clockwise then it will stop at 2+122=82+122=8.
(c) starts at
55
and makes
1414
of a revolution, clockwise?
Ans: When the hand of a clock starts at 55 and make 1414 of a revolution, clockwise then it will stop at 5+124=85+124=8.
(d) starts at
55
and makes
3434
of a revolution, clockwise?
Ans: When the hand of a clock starts at 55 and make 3434 of a revolution, clockwise then it will stop at 5+12×34=145+12×34=14 i.e., at 22 as one revolution is =12=12.
3. Which direction will you face if you start facing:
(a) East and make
1212
of a revolution clockwise?
Ans:
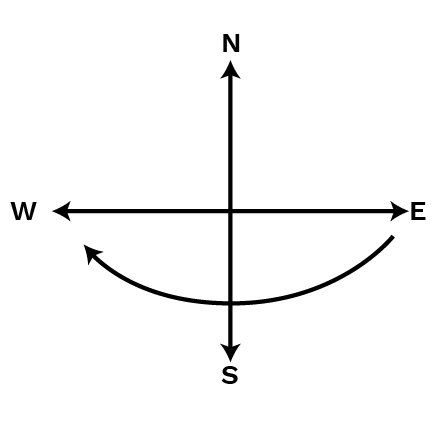
When we will make 1212 of a revolution, clockwise from east, then we will face the west direction.
(b) East and make
112112
of a revolution clockwise?
Ans: When we will make 112112 of a revolution, clockwise from east, then we will face the west direction.
(c) West and makes
3434
of a revolution clockwise?
Ans:
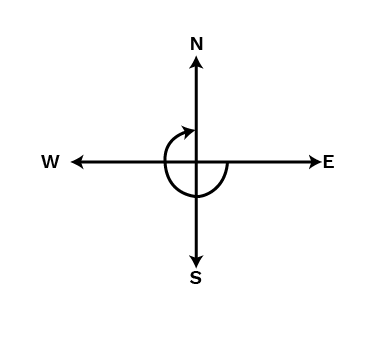
When we will make 3434 of a revolution, clockwise from west, then we will face the north direction.
(d) South and make one full revolution?
Ans:
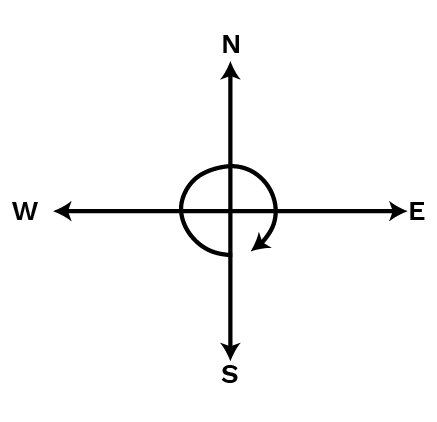
When we will make a one full revolution from south, then we will face the south direction. There will be no need for mentioning clockwise or anti-clockwise because anyhow one full revolution will bring us back to the original direction.
4. What part of a revolution have you turned through if you stand facing –
(a) East and turn clockwise to face north?
Ans:
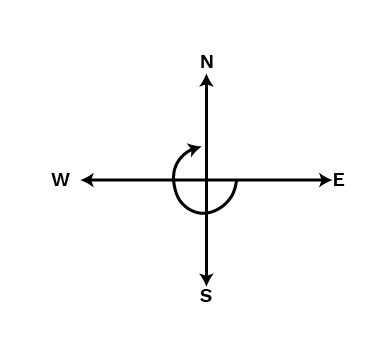
When we will turn clockwise from east to face north, then the revolution will be 3434.
(b) South and turn clockwise to face east?
Ans:
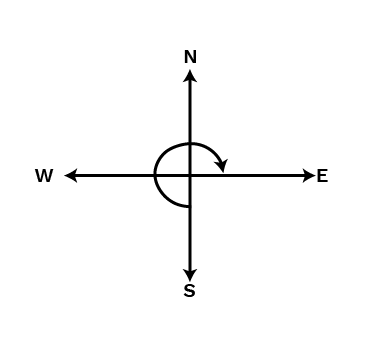
When we will turn clockwise from south to face east, then the revolution will be 3434.
(c) West and turn clockwise to face east?
Ans:
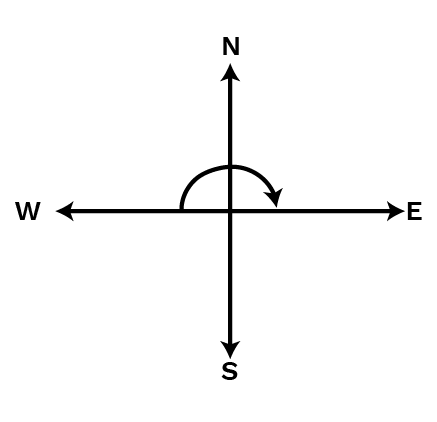
When we will turn clockwise from west to face east, then the revolution will be 1212.
5. Find the number of right angles turned through by the hour hand of a clock
(a) when it goes from
33
to
66
.
Ans: When the hour hand of a clock goes from 33 to 66 then the number of right angles turned will be one.
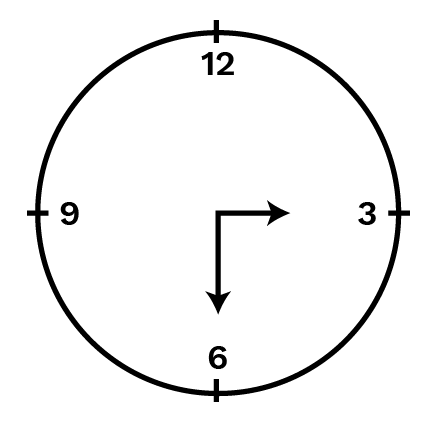
(b) when it goes from
22
to
88
.
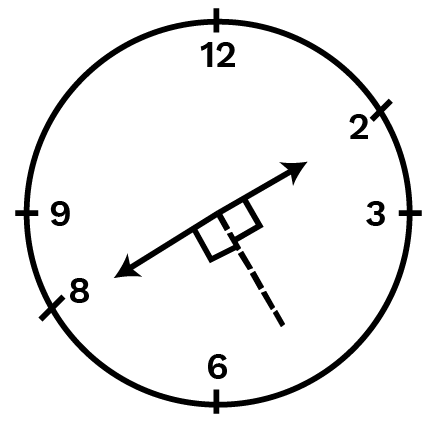
Ans: When the hour hand of a clock goes from 22 to 88 then the number of right angles turned will be two.
(c) when it goes from
55
to
1111
.
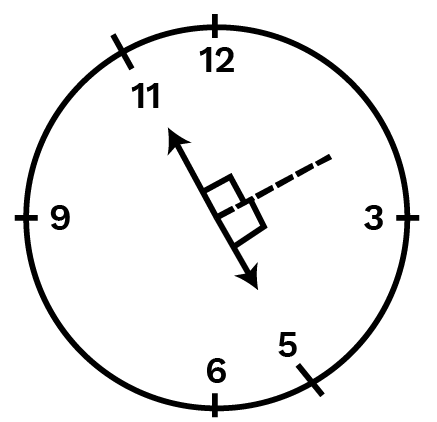
Ans: When the hour hand of a clock goes from 55 to 1111 then the number of right angles turned will be two.
(d) when it goes from
1010
to
11
.
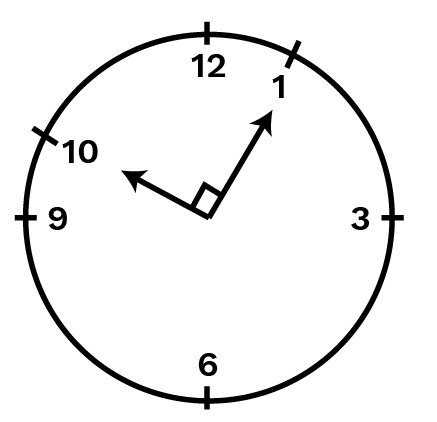
Ans: When the hour hand of a clock goes from 1010 to 11 then the number of right angles turned will be one.
(e) when it goes from
1212
to
99
.
Ans: When the hour hand of a clock goes from 1212 to 99 then the number of right angles turned will be three.
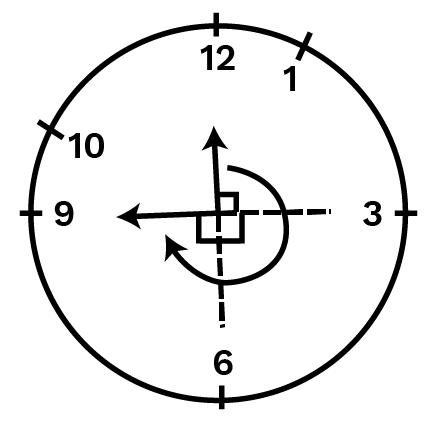
(f) when it goes from
1212
to
66
.
Ans: When the hour hand of a clock goes from 1212 to 66 then the number of right angles turned will be two.
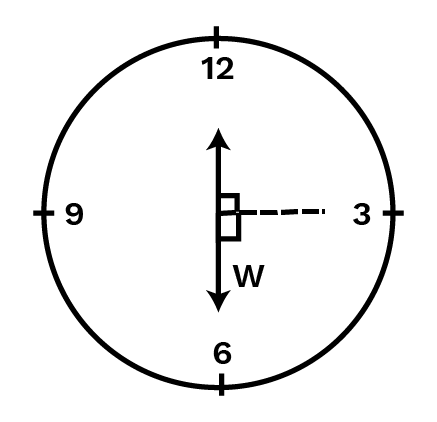
6. How many right angles do you make if you start facing –
(a) South and turn clockwise to west?
Ans: When we start facing south and turn clockwise to west then the number of right angles turned will be one.
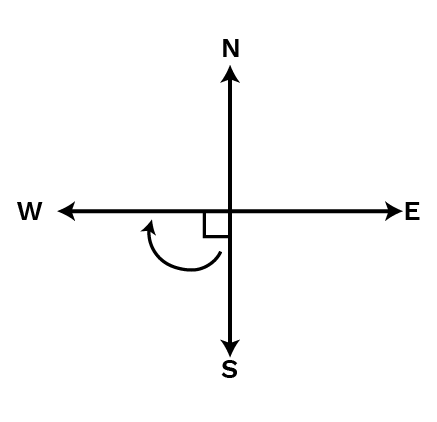
(b) North and turn anti-clockwise to east?
Ans: When we start facing north and turn anti-clockwise to east then the number of right angles turned will be three.
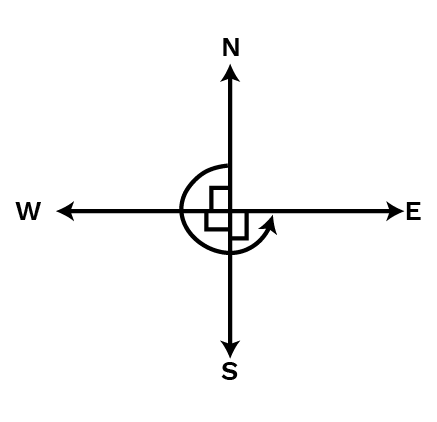
(c) West and turn to west?
Ans: When we start facing west and turn to west then the number of right angles turned will be four.
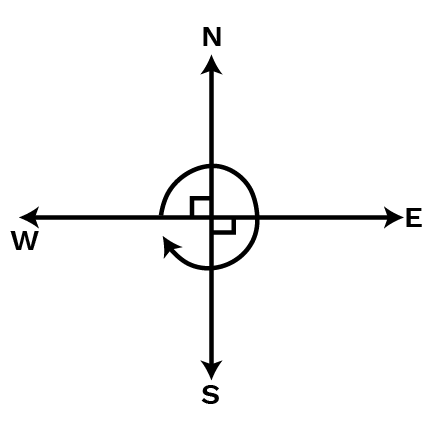
(d) South and turn to north?
Ans: When we start facing south and turn to north then the number of right angles turned will be two.
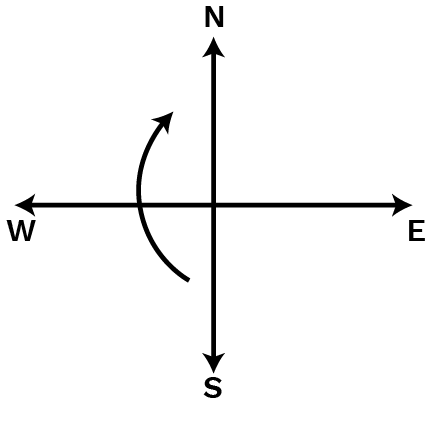
7. Where will the hour hand of a clock stop if it starts:
(a) from
66
and turns through
11
right angle?
Ans: One right angle = One-fourth of complete rotation of a clock 14×12=314×12=3
When the hour hand of a clock starts from 66 and turns through 11 right angle, then it will stop at 6+3=96+3=9.
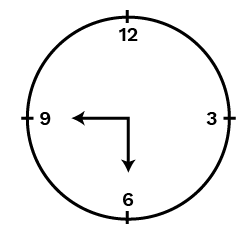
(b) from
88
and turns through
22
right angles?
Ans: One right angle = One-fourth of complete rotation of a clock 14×12=314×12=3
When the hour hand of a clock starts from 88 and turns through 22 right angles, then it will stop at 8+3+3=148+3+3=14 i.e., at 22.
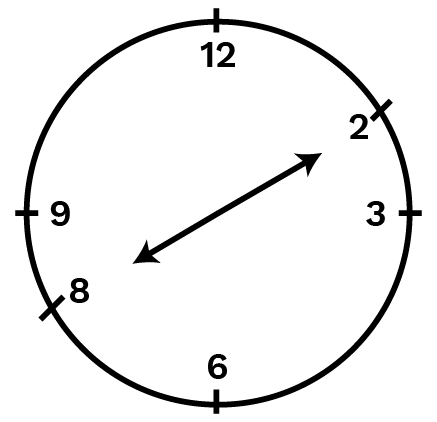
(c) from
1010
and turns through
33
right angles?
Ans: One right angle = One-fourth of complete rotation of a clock 14×12=314×12=3
When the hour hand of a clock starts from 1010 and turns through 33 right angles, then it will stop at 10+3+3+3=1910+3+3+3=19 i.e., at 7$.
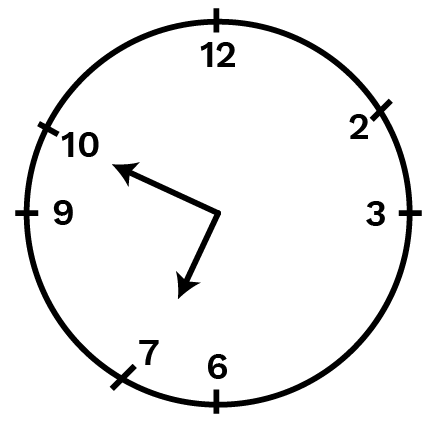
(d) from
77
and turns through
22
straight angles?
Ans: One Straight angle = 2 right angles
When the hour hand of a clock starts from 77 and turns through 22 straight angles, then it will stop at 7+6+6=197+6+6=19 i.e., at 7.
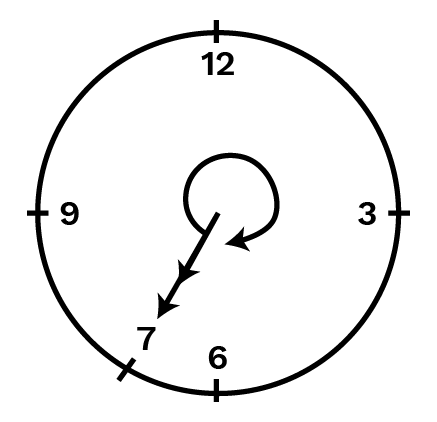
Exercise 5.3
1. Match the following:
| (i) Straight angle | (a) less than one-fourth a revolution |
| (ii) Right angle | (b) more than half a revolution |
| (iii) Acute angle | (c) half of a revolution |
| (iv) Obtuse angle | (d) one-fourth a revolution |
| (v) Reflex angle | (e) between 1414 and 1212 of a revolution |
| (f) one complete revolution |
Ans:
| (i) Straight angle | (c) half of a revolution |
| (ii) Right angle | (d) one-fourth a revolution |
| (iii) Acute angle | (a) less than one-fourth a revolution |
| (iv) Obtuse angle | (e) between 1414 and 1212 of a revolution |
| (v) Reflex angle | (b) more than half a revolution |
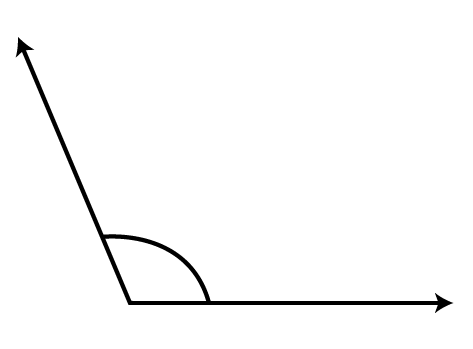
2. Classify each one of the following angles as right, straight, acute, obtuse or reflex:
(a)
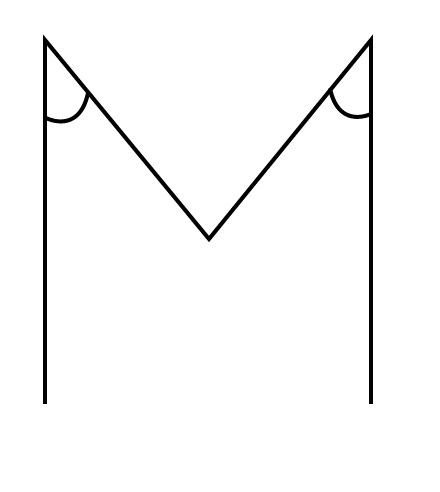
Ans: It is an acute angle.
(b)
Ans: It is an obtuse angle.
(c)
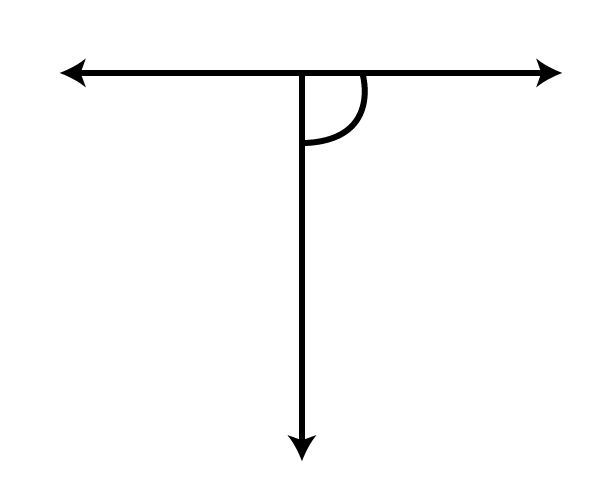
Ans: It is a right angle.
(d)
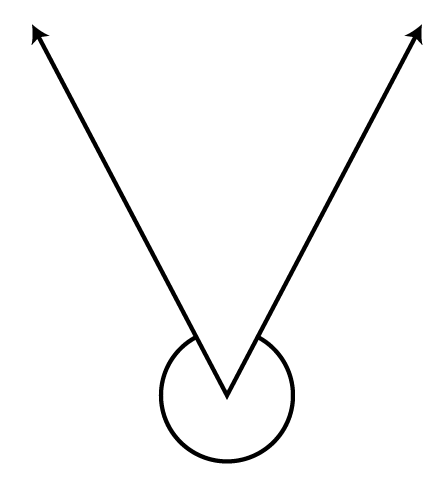
Ans: It is a reflex angle.
(e)
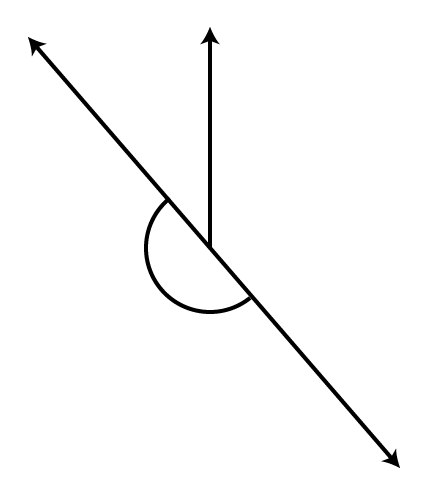
Ans: It is a straight angle.
(f)

Ans: It is an acute angle.
Exercise 5.4
1. What is the measure of –
(i) a right angle?
Ans: The measure of a right angle is 90∘90∘.
(ii) a straight angle?
Ans: The measure of a straight angle is 180∘180∘.
2. Say True or False:
(a) The measure of an acute angle
<90∘<90∘
.
Ans: True.
As, we measure any acute angle, then it will always be less than a right angle.
(b) The measure of an obtuse angle
<90∘<90∘
.
Ans: False.
When we measure an obtuse angle, then it will always be more than a right angle.
(c) The measure of a reflex angle
>180∘>180∘
.
Ans: True.
A reflex angle is always more than the measure of a straight line.
(d) The measure of a complete revolution
=360∘=360∘
.
Ans: True.
When we complete one revolution, it is measured as turn of two straight lines.
(e) If
m∠A=53∘�∠�=53∘
and
m∠B=35∘�∠�=35∘
, then
m∠A>m∠B�∠�>�∠�
.
Ans: True.
3. Write down the measure of:
(a) some acute angles
Ans: As, an acute angle is measured as less than a right angle. Therefore, some of the acute angles will be 45∘45∘, 30∘30∘, and etc.
(b) some obtuse angles
Ans: As, an obtuse angle is measured as more than a right angle. Therefore, some of the obtuse angles will be 105∘105∘, 140∘140∘, and etc.
4. Measure the angles given below, using the protractor and write down the measure:
(a)
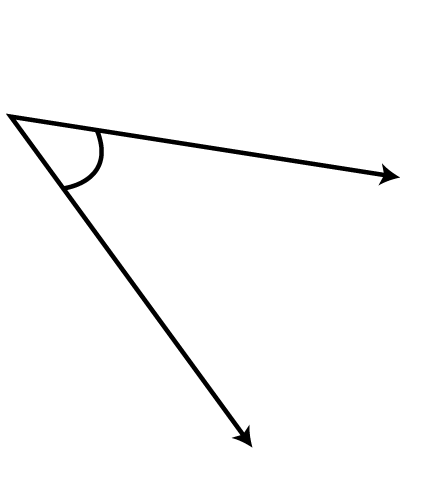
Ans: After using the protractor, we can conclude that the given figure is an acute angle measured as 40∘40∘.
(b)
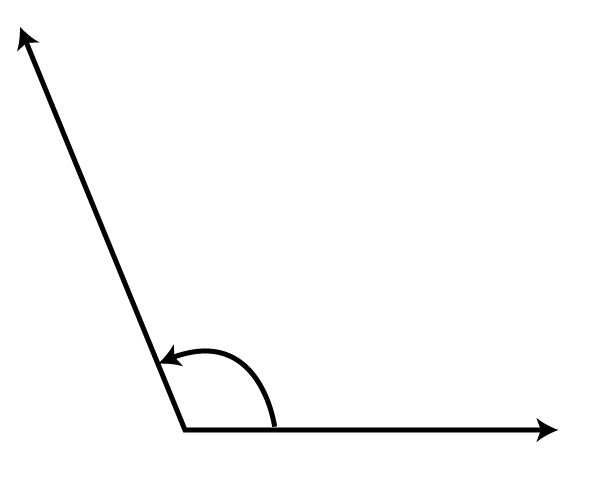
Ans: After using the protractor, we can conclude that the given figure is an obtuse angle measured as 130∘130∘.
(c)
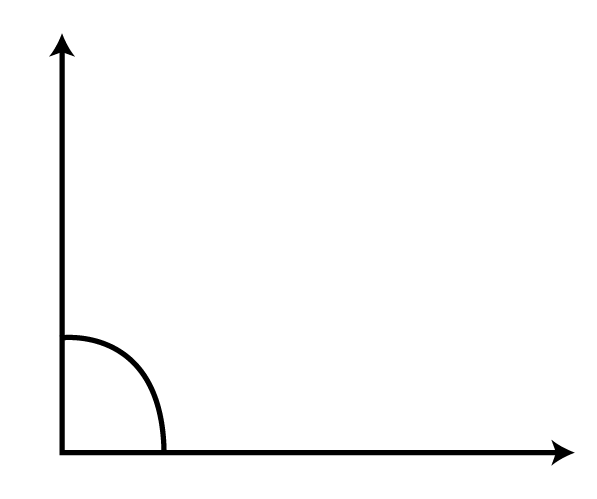
Ans: After using the protractor, we can conclude that the given figure is a right angle measured as 90∘90∘.
(d)
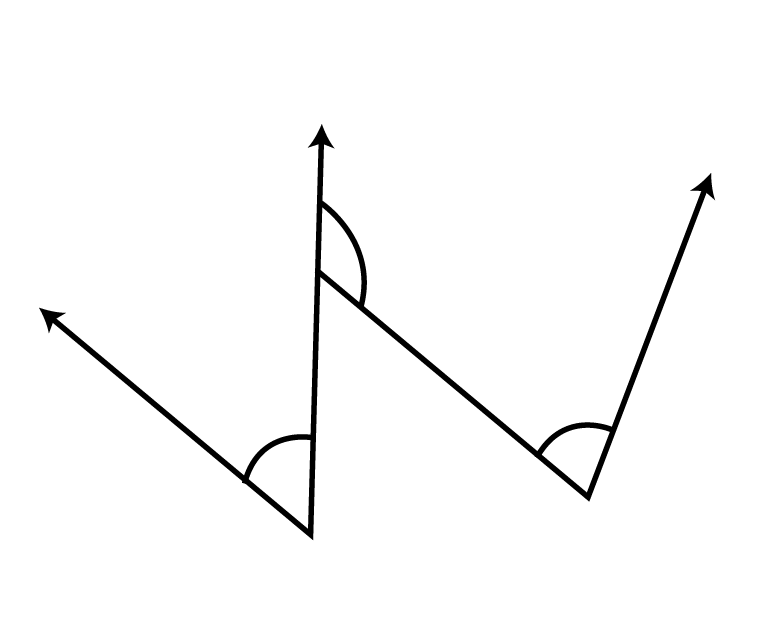
Ans: After using the protractor, we can conclude that the given figure is an acute angle measured as 60∘60∘.
5. Which angle has a large measure? First estimate and then measure:
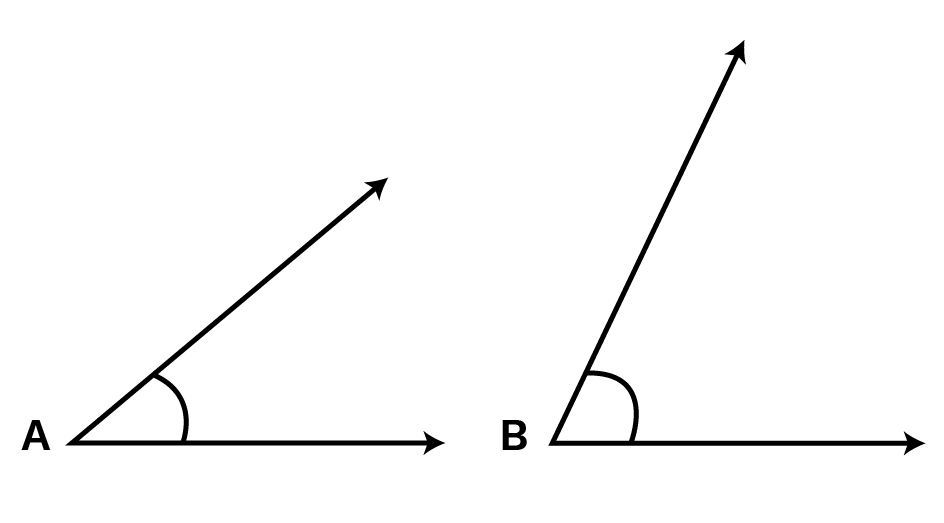
Ans: After estimating we can conclude that the measure of angle B� is larger than the measure of angle A�.
Measure of angle
A=�=
The measure of angle A� is 40∘40∘.
Measure of angle
B=�=
The measure of angle B� is 65∘65∘.
6. From these two angles which has larger measure? Estimate and then confirm by measuring them –
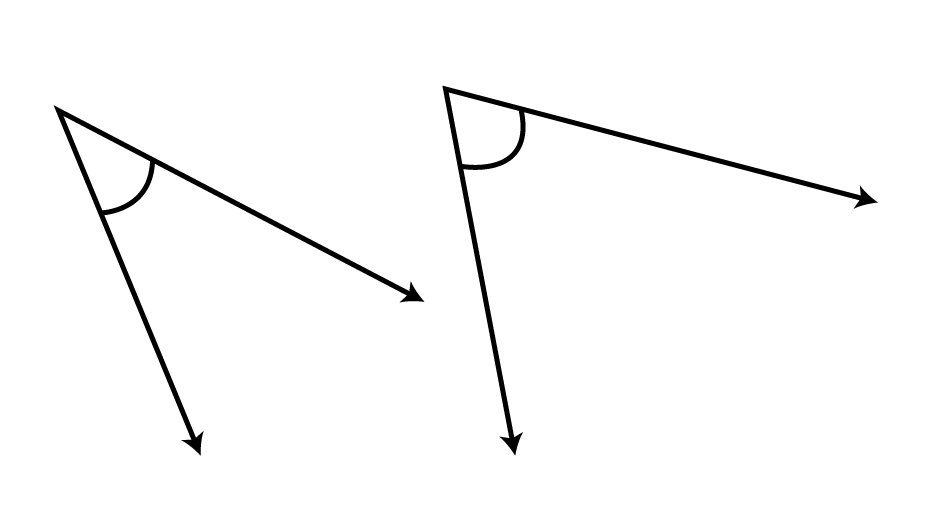
Ans: From the given figure we can estimate that the second angle has a larger measure than the first angle. After using the protractor, the measure of first angle is 45∘45∘ and the measure of second angle is 60∘60∘.
7. Fill in the blanks with acute, obtuse, right, or straight:
(a) An angle whose measure is less than that of a right angle is __________.
Ans: An angle whose measure is less than that of a right angle is acute angle.
(b) An angle whose measure is greater than that of a right angle is __________.
Ans: An angle whose measure is greater than that of a right angle is obtuse angle.
(c) An angle whose measure is the sum of the measures of two right angles is __________.
Ans: An angle whose measure is the sum of the measures of two right angles is straight angle.
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is __________.
Ans: When the sum of the measures of two angles is that of a right angle, then each one of them is acute angle.
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be ___________.
Ans: When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be obtuse angle.
8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor).
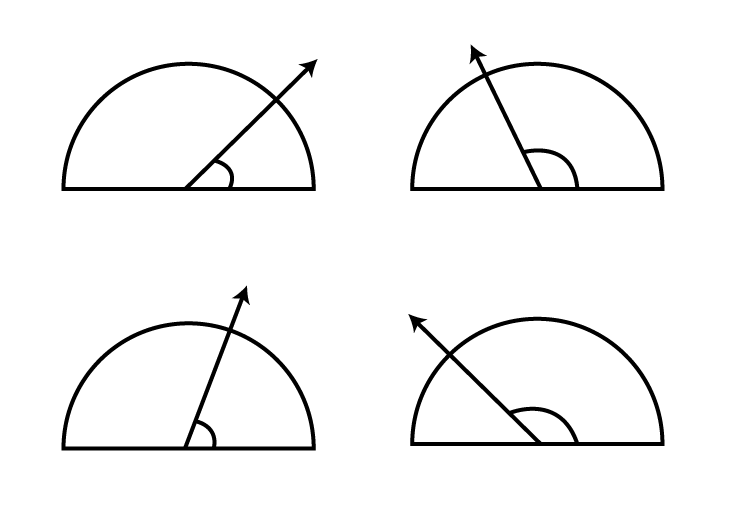
Ans: After estimating the measure of each angle shown in figure, we have –
(i) 30∘30∘
(ii) 120∘120∘
(iii) 60∘60∘
(iv) 150∘150∘
9. Find the angle measure between the hands of the clock in each figure:
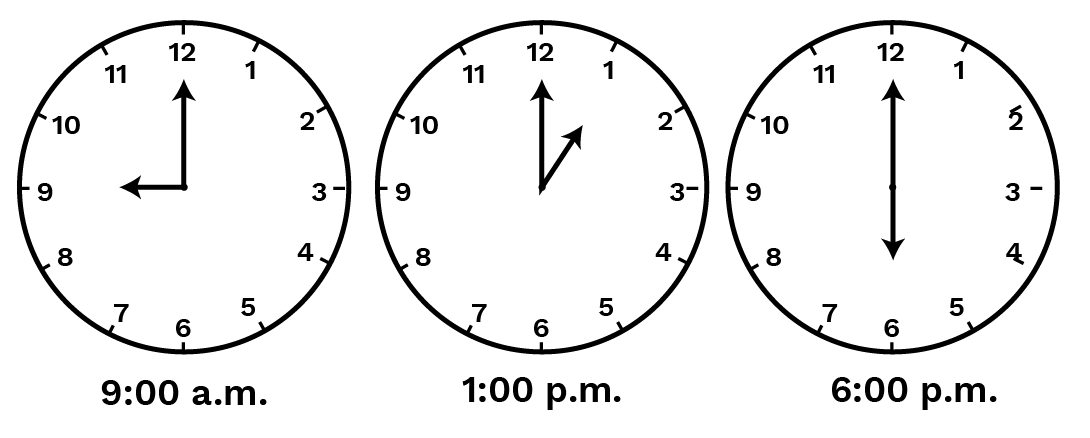
Ans: From the given figure, as the revolution is of 1414 from 99 to 1212 hence, the measure of the angle in first figure will be of 90∘90∘, second figure has angle of measure 30∘30∘ as each division is equal and the third figure has angle of measure 180∘180∘ as the revolution is of 1212 which will form a straight line.
10. Investigate:
In the given figure, the angle measure
30∘30∘
. Look at the same figure through a magnifying glass. Does the angle become larger? Does the size of the angle change?
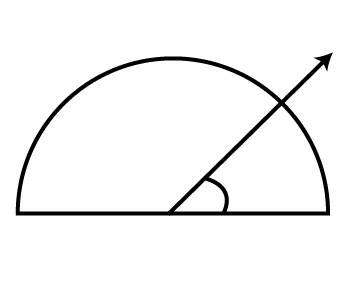
Ans: No, the size of the angle does not change and hence, remains same even after using the magnifying glass.
11. Measure and classify each angle:
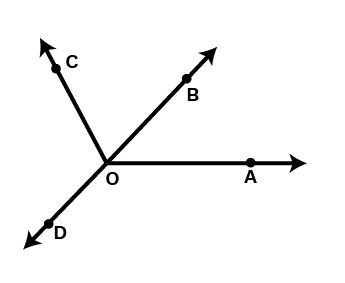
Ans: The measure of each angle can be measured by the help of a protractor. Hence, the angles will be –
Exercise 5.5
1. Which of the following are models for perpendicular lines –
(a) The adjacent edges of a tabletop.
Ans: Yes, adjacent edges of a table top are perpendicular.
(b) The lines of a railway track.
Ans: No, the lines of a railway track are not perpendicular.
(c) The line segments forming the letter ‘
L�
’.
Ans: Yes, the line segments forming the letter L� are perpendicular.
(d) The letter
V�
.
Ans: No, the letter V� is not perpendicular.
2. Let
PQ��
be the perpendicular to the line segment
XY��
. Let
PQ��
and
XY��
intersect in the point
A�
. What is the measure of
∠PAY∠���
.
Ans: As, PQ�� and XY�� are perpendicular line segments to each other and intersect at point A� can be shown in the figure below –
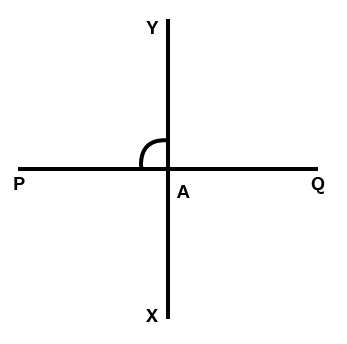
Therefore, the measure of ∠PAY=90∘∠���=90∘.
3. There are two “set-squares” in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
Ans: From the two “set-squares” in our box, we have one set-square as 30∘30∘, 60∘60∘, 90∘90∘ and another set-square as 45∘45∘, 45∘45∘, 90∘90∘. Therefore, the angle that is common is 90∘90∘.
4. Study the diagram. The line
l�
is perpendicular to line
m�
.

(a) Is
CE=EG��=��
?
Ans: As, CE=2 units��=2 units and
EG=2 units��=2 units. Therefore,
CE=EG��=��.
(b) Does
PE��
bisect
CG��
?
Ans: From the given figure we can conclude that yes, PE�� bisects CG��.
(c) Identify any two-line segments for which
PE��
is the perpendicular bisector.
Ans: Any two-line segments for which PE�� is the perpendicular bisector are DF�� and CG��.
(d) Are these true?
(i)
AC>FG��>��
Ans: Yes, it’s true. As, AC=2 units��=2 units and
FG=1 unit��=1 unit. Hence, AC>FG��>��.
(ii)
CD=GH��=��
Ans: Yes, it’s true. As, both CD�� and GH�� are of 1 unit1 unit.
(iii)
BC<EH��<��
Ans: Yes, it’s true. As, BC=1 unit��=1 ���� and
EH=3 units��=3 units. Hence, BC<EH��<��.
Exercise 5.6
1. Name the types of following triangles:
(a) Triangle with lengths of sides
7cm7��
,
8cm8��
and
9cm9��
.
Ans: As, all the three sides of the triangle have different lengths,
therefore, it is a scalene triangle.
(b)
ΔABCΔ���
with
AB=8.7cm��=8.7��
,
AC=7cm��=7��
and
BC=6cm��=6��
.
Ans: As, all the three sides of the triangle have different lengths, therefore, it is a scalene triangle.
(c)
ΔPQRΔ���
such that
PQ=QR=PR=5cm��=��=��=5��
.
Ans: As, all the three sides of the triangle have same lengths, therefore, it is an equilateral triangle.
(d)
ΔDEFΔ���
with
m∠D=90∘�∠�=90∘
.
Ans: Since, one of the angles of the triangle is 90∘90∘, therefore, it is a right-angled triangle.
(e)
ΔXYZΔ���
with
m∠Y=90∘�∠�=90∘
and
XY=YZ��=��
.
Ans: Since, one of the angles of the triangle is 90∘90∘, and two sides are of same length therefore, it is an isosceles right-angled triangle.
(f)
ΔLMNΔ���
with
m∠L=30∘�∠�=30∘
,
m∠M=70∘�∠�=70∘
and
m∠N=80∘�∠�=80∘
.
Ans: Since, all the angles of the triangle are less than right angle, therefore, it is an acute triangle.
2. Match the following: Measure of Triangle Types of Triangle
| (i) 33 sides of equal length | (a) Scalene |
| (ii) 22 sides of equal length | (b) Isosceles right angle |
| (iii) All sides are of different length | (c) Obtuse angle |
| (iv) 33 acute angles | (d) Right angle |
| (v) 11 right angle | (e) Equilateral |
| (vi) 11 obtuse angle | (f) Acute angle |
| (vii) 11 right angle with two sides | (g) Isosceles of equal length |
Ans:
| (i) 33 sides of equal length | (e) Equilateral |
| (ii) 22 sides of equal length | (g) Isosceles of equal length |
| (iii) All sides are of different length | (a) Scalene |
| (iv) 33 acute angles | (f) Acute angle |
| (v) 11 right angle | (d) Right angle |
| (vi) 11 obtuse angle | (c) Obtuse angle |
| (vii) 11 right angle with two sides | (b) Isosceles right angle |
3. Name each of the following triangles in two different ways: (You may judge the nature of angle by observation).
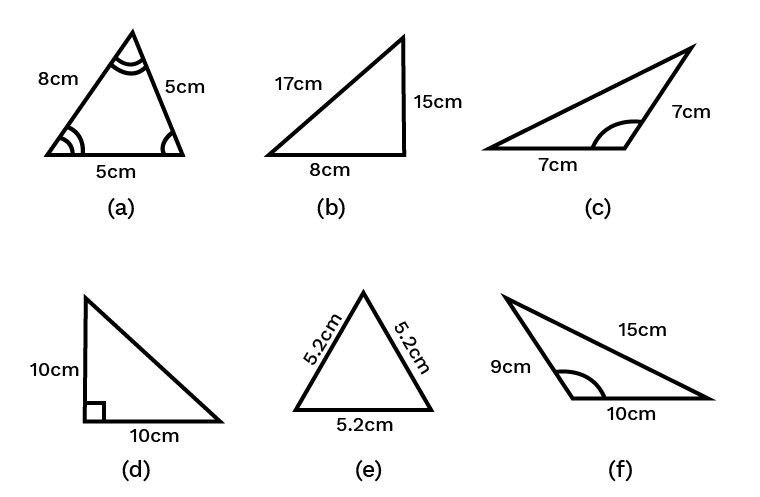
Ans: The triangles in two different ways will be as –
(a) Acute angled triangle and Isosceles triangle.
(b) Right-angled triangle and Scalene triangle.
(c) Obtuse-angled triangle and Isosceles triangle.
(d) Right-angled triangle and Isosceles triangle.
(e) Equilateral triangle and acute angled triangle.
(f) Obtuse-angled triangle and scalene triangle.
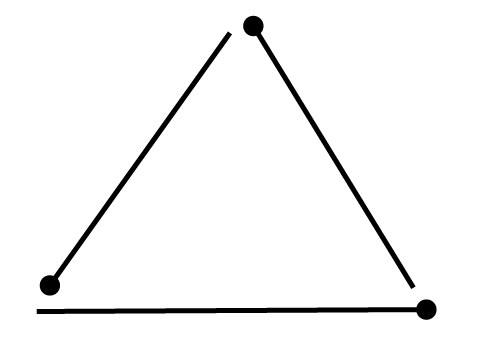
4. Can you make a triangle with
(a)
33
matchsticks – Triangle possible
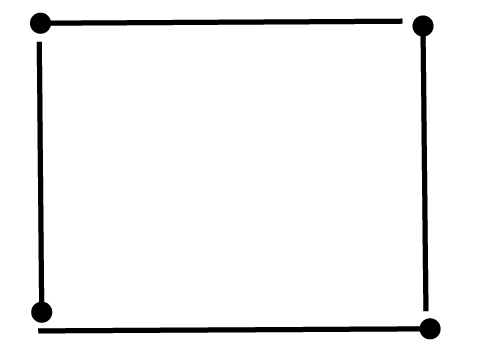
(b)
44
matchsticks – Triangle not-possible
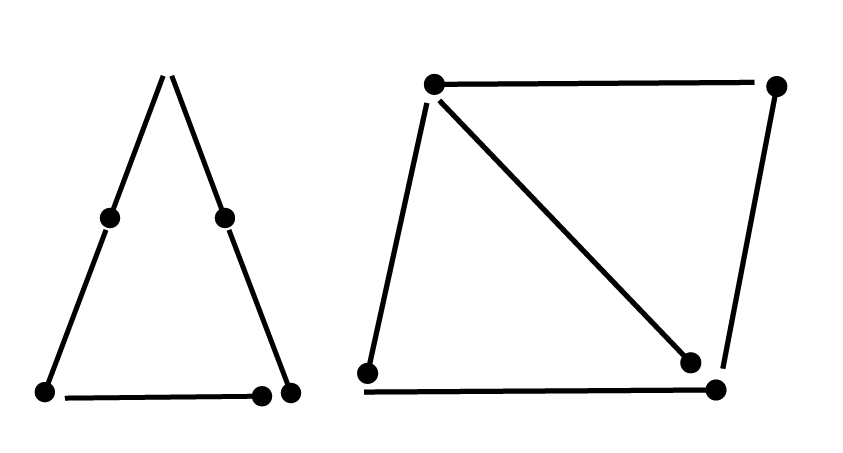
(c)
55
matchsticks – Triangle Possible
This is an acute angle triangle, and it is possible to make triangle with five matchsticks.
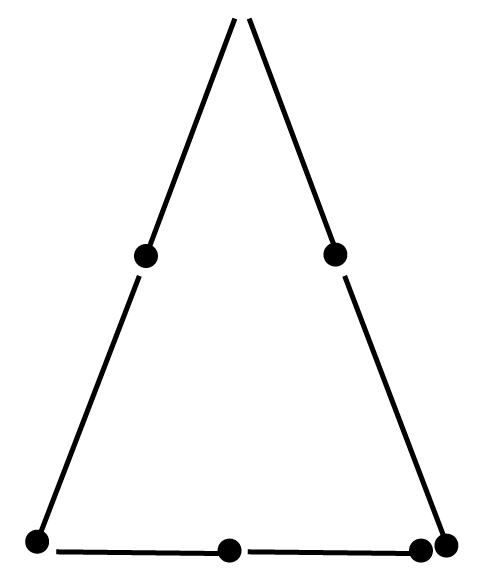
(d)
66
matchsticks – Triangle Possible
Exercise 5.7
1. Say true or false:
(a) Each angle of a rectangle is a right angle.
Ans:
True. Each side of a rectangle is a right angle.
(b) The opposite sides of a rectangle are equal in length.
Ans:
True. Opposite sides of a rectangle are always equal and parallel to each other.
(c) The diagonals of a square are perpendicular to one another.
Ans:
True. Square has diagonals that are bisecting each other at 90∘90∘.
(d) All the sides of a rhombus are of equal length.
Ans:
True. Rhombus has all sides of equal length.
(e) All the sides of a parallelogram are of equal length.
Ans:
False. Not all sides of a parallelogram are of equal length.
(f) The opposite sides of a trapezium are parallel.
Ans: False. Opposite sides of a trapezium are never equal.
2. Give reasons for the following:
(a) A square can be thought of as a special rectangle.
Ans: As, opposite sides of a rectangle are equal, and all angles are 90∘90∘. Therefore, we can say square as a special rectangle with all sides of equal length and all angles as 90∘90∘.
- A rectangle can be thought of as a special parallelogram.
Ans: As, both rectangle and parallelogram have opposite sides equal and parallel to each other. Therefore, we can say that rectangle can be a special parallelogram.
(c) A square can be thought of as a special rhombus.
Ans: Because both square and rhombus has all sides of same length and also their diagonals bisect each other at 90∘90∘. Therefore, a square can be a special rhombus.
(d) Squares, rectangles, parallelograms are all quadrilateral.
Ans: A quadrilateral is a shape that has at least 44 sides. Therefore, squares, rectangles, parallelograms are all types of quadrilaterals.
(e) Square is also a parallelogram.
Ans: Since, in parallelogram opposite sides are always equal and parallel to each other. Therefore, a square can also be a special parallelogram.
3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Ans: A square has its all sides in equal length and all angles are also equal. Therefore, a square is a regular quadrilateral.
Exercise 5.8
1. Examine whether the following are polygons. If anyone among these is not, say why?
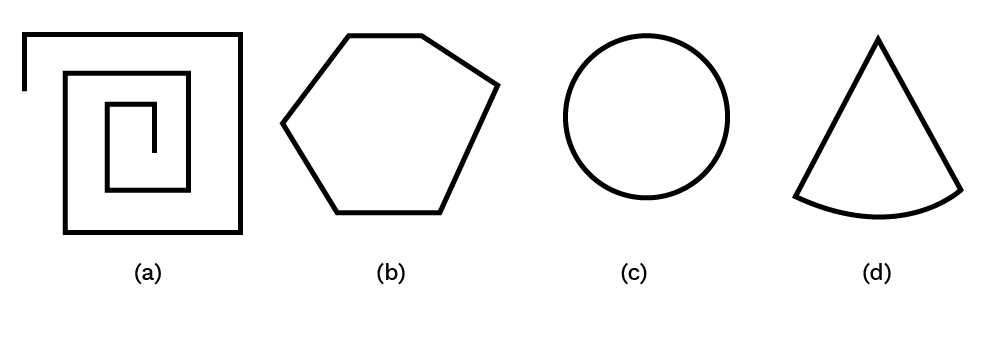
Ans: As, the figure in (a)(�) is not close, hence, it cannot be a polygon. Whereas figure (b)(�) is a closed shape, hence, it is a polygon. Similarly, in figure (c)(�) and (d)(�) as the shape is not enclosed by line segments, therefore, they are also not polygons.
2. Name each polygon:
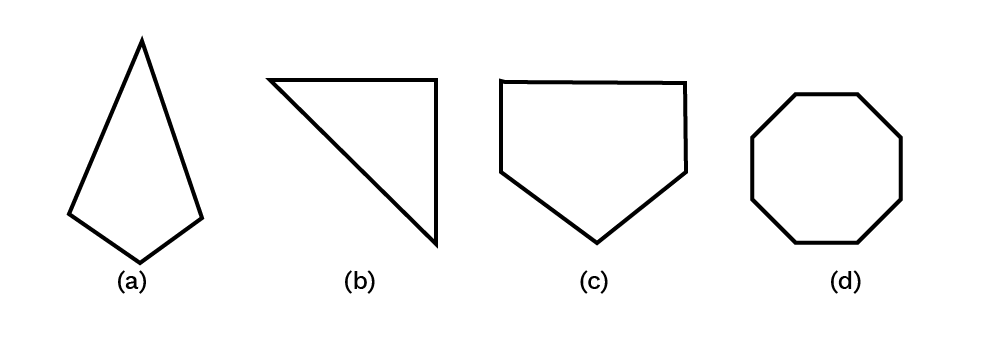
Ans: The polygon in figure (a)(�) is a quadrilateral as it has four sides, in figure (b)(�) it is a triangle as it has three sides, in figure (c)(�) it is a pentagon as it has five sides and in figure (d)(�) it is a octagon as it has eight sides.
3. Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
Ans: A rough sketch of a regular hexagon with connecting any three of its vertices and drawing a triangle will be as –
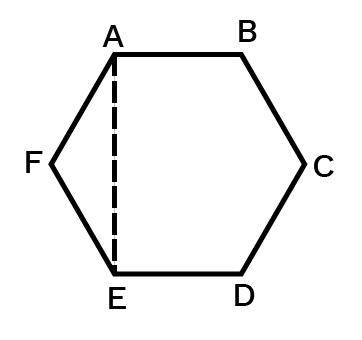
So, we have joined three vertices A�, E�, and F�. Therefore, the triangle formed is an isosceles triangle as two sides are equal.
4. Draw a rough sketch of a regular octagon. (Use squared paper if you wish). Draw a rectangle by joining exactly four of the vertices of the octagon.
Ans: A rough sketch of a regular octagon when a rectangle is drawn using any of its four vertices will be as –
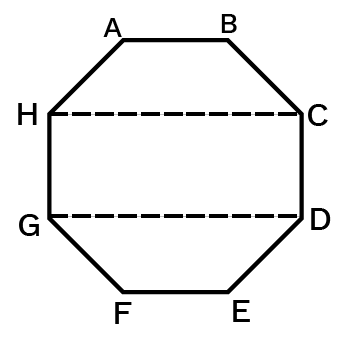
Here, CDGH���� is a rectangle.
5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
Ans: A rough sketch of a pentagon with its diagonals will be as –
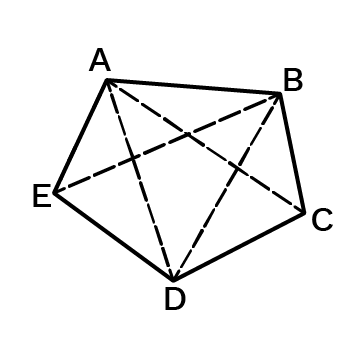
Here, ABCDE����� is a pentagon which has diagonals as AD��, AC��, BE��, and BD��.
Exercise 5.9
1. Match the following:
(a) Cone

(b) Sphere

(c) Cylinder

(d) Cuboid

(e) Pyramid

Give two example of each shape.
Ans:
(a) Cone

Examples are birthday caps, ice-cream cone, etc
(b) Sphere

Examples are ball, orange, etc.
(c) Cylinder

Examples are bottles, cylinder, etc.
(d) Cuboid

Examples are books, geometry box, etc.
(f) Pyramid

Examples are tent, tower, etc.
2. What shape is:
(a) Your instrument boxes?
Ans: Instrument boxes are of cuboid shape.
(b) A brick?
Ans: A brick is cuboid shaped.
- A match box?
Ans: A match box has shape of a cuboid.
- A road-roller?
Ans: Road roller has cylindrical shape.
- A sweet laddu?
Ans: A sweet laddu is of spherical shape.
NCERT Solutions for Class 6 Maths Chapter 5 – Understanding Elementary Shapes
NCERT Solutions Class 6 Maths Chapter 5 – Free PDF Download
Chapter 5 of Class 6 Mathematics discusses various shapes that exist in the world around us. It is imperative for students to have a clear understanding of different geometrical shapes, and this solution helps them in this process.
This chapter has a total of ten topics, and each of them tackles a different concept. It begins with the measurement technique of different line segments and then moves into more advanced concepts of angles and various geometrical shapes.
NCERT Solutions for Class 6 Maths Chapter 5 are a vital study material for students of class six. It offers comprehensive yet easy to understand insight into this important concept of mathematics. It helps students to comprehend the topics quickly and improve their exam preparations.
NCERT Solution for Class 6 Maths Chapter 5 Topic-Wise Discussion
Class 6 Maths chapter 5 has ten sub-topics, and here is a brief idea of each topic –
1. Introduction
The chapter begins with an introduction to various geometric shapes and how they are created with different lines. It talks about how shapes use straight lines, curved lines, etc. This chapter allows a more in-depth Understanding of Elementary shapes Class 6 with real-life examples.
2. Measuring Line Segment
A line segment is a portion of any lines that one can draw. In this chapter, students will learn how to measure different types of lines and tools necessary for the job. Along with that, they will also learn how to compare between various line segments in this chapter of NCERT Class 6 Maths Chapter 5.
3. Angles – Right and Straight
The next sub-topic in this NCERT Maths Book Class 6 Chapter 5 solutions talks about a vital concept of geometry, angles. In this particular section, students learn about two important angles, right-angle and straight-angle.
A right-angle is of 90 degrees, and a straight-angle is of 180 degrees. There are various examples of directions and the position of clock hands to make this concept clear to the students.
4. Angles – Acute, Obtuse, Reflex
Apart from right-angle and straight-angle, there are three primary classifications of angles, these are –
- Acute angle, which is less than the right-angle.
- Obtuse angle, which is higher than a right-angle but lower than a straight-angle.
- Reflex angle, which is higher than a straight-angle.
The fourth section of NCERT Class 6 Maths Chapter 5 provides a detailed look into these three angles. There are various real-life examples to make these concepts more relatable to the students.
5. Measuring Angles
Class 6 Understanding Elementary Shapes further includes the discussion of angle measurement. In this section, students will learn how to measure various angles effectively. They will learn the use of a protractor, and how it helps in accurate measurement of different angles.
6. Perpendicular Lines
When two lines intersect each other at a right angle, they are called perpendicular lines. The next chapter of Elementary Shapes Class 6, includes a detailed discussion of this topic.
7. Classification of Triangles
In this sub-topic of NCERT Solutions for Class 6 Maths Chapter 5, candidates will know in detail about various triangles. Along with their properties, students will also learn how to name triangles based on their sides and the degree of their angles.
This section includes an introduction to types of triangles like scalene, isosceles, equilateral, etc. named as per the sides of a triangle. Along with them, students will also learn about different triangle names based on their angle size like a right-angle triangle, obtuse-angled triangle, acute-angle triangle, etc.
8. Quadrilaterals
A quadrilateral is nothing but a polygon with four sides. However, there is more to that, and in this Class 6th Maths Chapter 5 students will know about it in detail. Students can use the set-squares to form various quadrilaterals.
9. Polygon
Class 6 Maths Understanding Elementary Shapes further discusses the concept of a polygon in its next section. A triangle and a quadrilateral is also a polygon with 3 and 4 sides respectively. In this particular discussion, students will come across other polygon types like pentagon, hexagon, and octagon. There are a few real-life examples of polygon resented as well in this chapter, to help students understand.
10. Three-Dimensional Shapes
Lastly, the CBSE Class 6 Maths Chapter 5 includes a discussion about 3-D shapes. Students have already studied about 2-D shapes till now, but now they will move on to more advanced concepts. These three-dimensional shapes are everywhere in the surroundings, and the use of them as an example helps students to comprehend such complicated topics easily.
It also includes an extensive discussion on the number of edges, faces, and vertices 3-D figures have.
We Cover All Exercises In The Chapter Given Below
EXERCISE 5.1 – 7 Questions with Solutions
EXERCISE 5.2 – 7 Questions with Solutions
EXERCISE 5.3 – 2 Questions with Solutions
EXERCISE 5.4 – 11 Questions with Solutions
EXERCISE 5.5 – 4 Questions with Solutions
EXERCISE 5.6 – 4 Questions with Solutions
EXERCISE 5.7 – 3 Questions with Solutions
EXERCISE 5.8 – 5 Questions with Solutions
EXERCISE 5.9 – 2 Questions with Solutions.
Know the Reasons to Study NCERT Solution Class 6 Maths Chapter 5
Here are some prominent reasons why NCERT Solutions for Class 6 Maths Chapter 5 is a must-read for students –
- These NCERT solutions follow the curriculum drafted by CBSE. Thus, their answers are in accordance with the requirements of CBSE.
- The language used here is simple and easy to understand. Hence, it is easier for students to comprehend any topic.
- The solutions provided in Chapter 5 Maths Class 6 NCERT Solutions are detailed, which will help students to gather all the necessary information.
- Additionally, the use of practical examples makes things easy to understand for students.
NCERT Solutions for Class 6 Maths Chapter 5 are readily available online for free. Students can download it from the website of Vedantu.
Conclusion
Study Studio’s NCERT Solutions for Class 6 Maths Chapter 5 – “Understanding Elementary Shapes” provide an essential resource for young learners. These solutions are thoughtfully designed to align seamlessly with the NCERT curriculum, ensuring that students receive clear explanations and step-by-step guidance in understanding geometric concepts. By offering practical insights into elementary shapes, these solutions empower students to grasp the fundamentals of geometry effectively. Study Studio’s commitment to quality education shines through in these solutions, making them a crucial tool for Class 6 students. By utilizing these NCERT Solutions, students can strengthen their mathematical skills, develop spatial reasoning abilities, and foster a solid foundation in geometry, all of which are essential for their academic growth.