Download the NCERT Solutions for Class 4 Maths Chapter 11 Tables and Shares, drafted by the highly experienced teachers at Study Studio and help your child with a simplified learning experience. As the name of Chapter 11 Tables and Shares suggests, it covers the concepts of division, multiplication, and distribution. By referring to these NCERT Solutions for Class 4 Chapter 11 Tables and Shares students can learn easy problem-solving methods for the sums of this chapter.
NCERT Solutions for Class 4 Maths Chapter 11 – Tables and Shares deals with multiplication and division.
Access NCERT Solutions for Class 4 Chapter 11 – Tables and Shares
1 .What are the ways in which the sunflower and marigold are planted?
18 = ______ × ______
So, there are ______ rows with ______ plants each.
18 = ______ × ______
So, there are ______ rows with ______ plants each.
Ans : Here,
18=1×1818=1×18, so there is 1 row with 18 plants.
18=2×1918=2×19, so there are 2 rows with 9 plants each.
2.Jars in the Shelf Bheema made a shelf for 30 jars. This is a long shelf with two rows. Each row has the same number of jars. Can you think of other ways to make a shelf to keep 30 jars?
Draw a shelf. Show how many jars you will keep in each row. How many rows are there?
Have your friends drawn it in different ways?
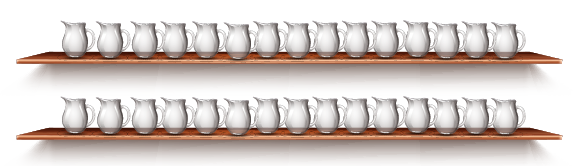
Ans: Yes, we can make a shelf in 3 rows in which each row has 10 jars. The shelf looks like as given below figure :
Number of jars in each row =30÷3=10=30÷3=10

The other ways to keep the jars as follows
5 rows containing 6 jars in a row
6 rows containing 5 jars in a row
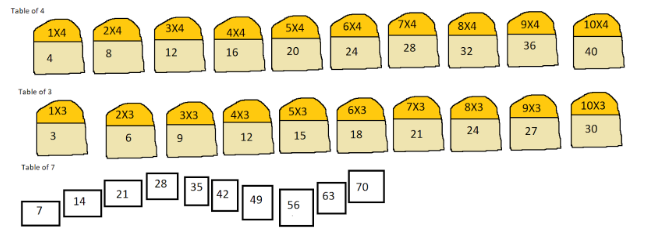
3. Help Bunty to make the table of 7, using tables of 4 and 3.
Ans : Here for solving this,
We will use the tables of 4 and 3 for writing the table of 7.
Pictorial representation :
4. Which two tables will you use for writing the table of 12?
Ans: Here for solving this,
We will use the tables of 5 and 7 for writing the table of 12.
The table of 5 is given below:

The table of 7 is given below:

Now, the table 12 has become as given below:
| 5+75+7 | 10+1410+14 | 15+2115+21 | 20+2820+28 | 25+3525+35 | 30+4230+42 |
| 12 | 24 | 36 | 48 | 60 | 72 |
| 35+4935+49 | 40+5640+56 | 45+6345+63 | 50+7050+70 |
| 84 | 96 | 108 | 120 |
Pictorial Representation :

5.
| How many legs ? | 4 | 8 | 12 | |||||
| How many cats ? | 1 | 2 |
So 28 legs mean _______ cats.
Ans : Here,
Number of legs of 1 cat =1×4=4=1×4=4
Number of legs of 2 cats =2×4=8=2×4=8
Number of legs of 3 cats =3×4=12=3×4=12
After reading the above data , we can easily fill the given table :
| How many legs ? | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
| How many cats ? | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
So, from the table we can see that 7 cats have 28 legs.
6.Billo has kept his chickens in a box. He counted 28 legs. How may chickens are there ?
Ans: A chicken has 2 legs. So, If there are total 28 legs then the number of chickens kept in the box :
=28÷2=14=28÷2=14
| How many legs ? | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 |
| How many chickens? | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
From the table, we can see 14 chickens have 28 legs.
Thus, 14 chickens are there in the box.
7. Leela has not gone to school for 21 days. For how many weeks was she away from school?
Ans: Number of days Leela did not go to school =21=21days.
A week has 7 days so the number of weeks Leela did not go to school =21÷7=3=21÷7=3
37)21¯¯¯¯¯−210¯¯¯37)21¯−210¯
| How Many Days? | 7 | 14 | 21 |
| How Many Weeks? | 1 | 2 | 3 |
Here, 21 days means 3 weeks.
Thus, Leela did not go to school for 3 weeks.
8. A frog jumps 3 steps at a time starting from 0.
- Count the jumps he takes to reach 27. So, he has taken27÷3=27÷3=______ jumps.

He has taken _________ jumps, if he is at 36.
- If he is at 42, he has taken _________ jumps. Starting from 0, a rabbit jumps 5 steps at a time.
- In how many jumps does he reach 25? ____________
- He reaches ____________ after taking 8 jumps. • He needs ____________ jumps to reach 55.
Ans: Here,
- Number of jumps taken by the frog to cover 3 steps =1=1
Number of jumps taken by the frog to cover 27 steps = 27÷3=927÷3=9
So, he has taken 27÷3=927÷3=9 jumps.
- Number of jumps taken by the frog to cover 3 steps =1=1
Number of jumps taken by the frog to cover 36 steps =36÷12=3=36÷12=3
He has taken 12 jumps, if he is at 36.
- Number of jumps taken by the frog to cover 3 steps =1=1
Number of jumps taken by the frog to cover 42 steps =42÷3=14=42÷3=14
If he is at 42, he has taken 14 jumps.
- Number of jumps taken by the rabbit to cover 5 steps =1=1
Number of jumps taken by the frog to cover 25 steps =25÷5=5=25÷5=5
Thus, the rabbit will reach 25 in 5 jumps.
- Number of steps covered in 1 jump = 5
Number of steps covered in 8 jumps =5×8=40=5×8=40
He reaches 40 after taking 8 jumps.
- Number of jumps taken by the rabbit to cover 5 steps =1=1
Number of jumps taken by the frog to cover 55 steps =55÷5=11=55÷5=11
He needs 11 jumps to reach 55.
9. Practice Time
- 28÷2=28÷2=
Ans: 142)28¯¯¯¯¯−208¯¯¯¯¯−80¯¯¯142)28¯−208¯−80¯
- 56÷7=56÷7=
Ans :
87)56¯¯¯¯¯−560¯¯¯87)56¯−560¯
- 48÷4=48÷4=
Ans 124)48¯¯¯¯¯−408¯¯¯¯¯−80¯¯¯124)48¯−408¯−80¯
- 66÷6=66÷6=
Ans: 116)66¯¯¯¯¯−606¯¯¯¯¯−60¯¯¯116)66¯−606¯−60¯
- 96÷8=96÷8=
Ans: 128)96¯¯¯¯¯−816¯¯¯¯¯−160¯¯¯128)96¯−816¯−160¯
- 110÷10=110÷10=
Ans: 1110)110¯¯¯¯¯¯¯¯−1010¯¯¯¯¯−100¯¯¯1110)110¯−1010¯−100¯
10.He took 28 shells for one necklace. 112 − 28 = 84 Now he was left with 84 shells. Again he took 28 more shells for the second necklace.
- How many shells are left now? __________ Then he took shells for the third necklace.
- So he was left with ___________ shells.
- How many necklaces can Dhruv make from 112 shells? _________
- Are the shells enough for making necklaces for all his friends? ___________.
Ans: After making the first necklace, Dhruv was left with 84 shells.
Number of shells used for the second necklace =28=28
Number of shells left with Dhruv=84−28=56=84−28=56
Working: =84−28=56=84−28=56Thus, Dhruv was left with 56 shells after making the second necklace.
Dhruv took 28 more shells for making the third necklace.Number of shells left with
Dhruv after making third necklace =56−28=28=56−28=28
Dhruv made a necklace of 28 shells for each of his three friends.
After making the necklaces for his friends, he was left with 28 shells.
So, he could make one more necklace with the remaining shells. Thus, Dhruv could
make a total of 4 necklaces with 112 shells.
Yes, the number of shells were enough for making necklaces for all the friends. After
making 3 necklaces for his friends, 28 shells were still left with Dhruv.
11. Kannu made a necklace of 17 sea-shells. How many such necklaces can be made using 100 sea shells?
Ans: Total number of shells =100=100
Kannu made 1 necklace of 17 sea-shells.
Hence, number of shells left after making 1 necklace =100−17=83=100−17=83
shells left after making 2 necklace=83−17=66=83−17=66
shells left after making 3 necklace=66−17=49=66−17=49
shells left after making 4 necklace=49−17=32=49−17=32
shells left after making 5 necklace=32−17=15=32−17=15
Thus, 15 shells were left after making 5 necklaces.
Therefore, 5 necklaces can be made by using 100 sea shells.
12.One carton can hold 85 soap bars. Shally wants to pack 338 soap bars. How many cartons does she need for packing all of them?
Ans: Soap bars 1 carton can hold =85=85
Soap bars 2 cartons can hold=2×85=170=2×85=170
Soap bars 3 cartons can hold=3×85=255=3×85=255
Soap bars 4 cartons can hold =4×85=340=4×85=340
340 soaps can be accomodated in 4 cartons. Thus, 4 cartons will be needed to pack 338 soap bars.
13. Manpreet wants 1500 sacks of cement for making a house. A truck carries 250 sacks at a time. How many trips will the truck make?
A driver charges Rs 500 for a trip. How much will Manpreet pay the driver for all the trips?
Ans: Number of sacks a truck can carry at a time=250=250
In 2 trips number of sack carried=250×2=500=250×2=500
In 3 trips number of sack carried =250×3=750=250×3=750
In 4 trips number of sack carried =250×4=1000=250×4=1000
In 5 trips number of sack carried=250×5=1250=250×5=1250
In 6 trips number of sack carried =250×6=1500=250×6=1500
Thus, 6 trips are required to carry 1500 sacks.
14. Gangu’s Sweets Gangu is making sweets for Id. He has made a tray of 80 laddoos.

Are the sweets in the tray enough to pack 23 small boxes? ___________
- How many more sweets are needed? ___________
- Gangu also has a bigger box in which he packs 12 laddoos.
How many boxes does he need for packing 60 laddoos?
Ans: Number of laddoos in a smallbox =4=4
Number of laddoos needed to pack 23 small boxes =4×23=92=4×23=92
Total number of ladoos in the tray =80=80
No, the ladoos are not enough to pack in the boxes. There are 80 laddoos and 92 laddoos are required. Thus, Gangu is falling short of 12 laddoos.
As number of laddoos required to pack 23 small boxes =92=92
Number of laddoos available =80=80
Number of laddoos needed =92−80=12=92−80=12
Therefore, still 12 more laddoos are required to pack 23 small boxes.
15.Practice Time :Neelu brought 15 storybooks to her class. Today 45 students are present. How many children will need to share one book?
Ans: Neelu brought 15 storybooks to her class 45 students are present in the class
Total number of children sharing one book =45÷15=3=45÷15=3
Thus, 3 children need to share one book.
16.Practice Time: A family of 8 people needs 60 kg wheat for a month. How much wheat does this family need for a week?
Ans: In one month a family requires 60kg of wheat.
In a month, there are 4 weeks.
So, the quantity of wheat required in one week by the family=60÷4=60÷4kg =15=15kg
154)60¯¯¯¯¯−420¯¯¯¯¯−200¯¯¯154)60¯−420¯−200¯
Thus, the family needs 15 kg of wheat in one week.
17. Practice Time:

Time Razia wants change for Rs 500.
How many notes will she get if she wants in return.

- All 100 rupee notes? _________________

- All 50 rupee notes? __________________

(c) All 20 rupee notes? __________________

(d) All 5 rupee notes? ___________________
Ans:
- Total money with Razia=Rs500=��500
Razia wants a change for Rs 500 in the form of 100 rupee notes.
Number of 100 rupee notes that Razia will get =500÷100=5=500÷100=5
- Total money with Razia=Rs500=��500
Razia wants a change for Rs 500 in the form of 50 rupees notes.
Number of 50 rupees notes that Razia will get=500÷50=10=500÷50=10
- Total money with Razia=Rs500=��500
Razia wants a change for Rs 500 in the form of 20 rupees notes.
Number of 20 rupees notes that Razia will get =500÷20=25=500÷20=25
- Total money with Razia=Rs500=��500
Razia wants a change for Rs 500 in the form of 5 rupees notes.
Number of 5 rupee notes that Razia will get =500÷5=100=500÷5=100
18. Practice Time: You have to distribute 72 tomatoes equally in 3 baskets. How many tomatoes will there be in each?
Ans: If 72 tomatoes needed to be equally distributed in three baskets then each basket will contain
=72÷3=72÷3=24=24.
243)72¯¯¯¯¯−612¯¯¯¯¯−12 0¯¯¯243)72¯−612¯−12 0¯
Thus, 24 tomatoes will be there in each basket.
19. Practice Time There are 350 bricks in a hand-cart. Binod found the weight of a brick to be 2 kg. What will be the weight of all the bricks?
Ans : If the weight of 1 brick is 2 kg then the weight of 350 bricks
=2×350kg=700kg=2×350��=700��
Thus, the weight of all the bricks is 700kg.
20.Try Doing These :
(a) 65÷565÷5
Ans:
135)65¯¯¯¯¯−515¯¯¯¯¯−15 0¯¯¯135)65¯−515¯−15 0¯
(b) 84÷284÷2
Ans:
422)84¯¯¯¯¯−84¯¯¯−4 0¯¯¯422)84¯−84¯−4 0¯
(c) 69÷369÷3
Ans:
233)69¯¯¯¯¯−69¯¯¯−9 0¯¯¯233)69¯−69¯−9 0¯
(d) 90÷690÷6
Ans:
156)90¯¯¯¯¯−630¯¯¯¯¯−30 0¯¯¯156)90¯−630¯−30 0¯
(e) 72÷472÷4
Ans:
184)72¯¯¯¯¯−432¯¯¯¯¯−32 0¯¯¯184)72¯−432¯−32 0¯
(f) 108÷9108÷9
Ans:
123)108¯¯¯¯¯¯¯¯−618¯¯¯¯¯−18 0¯¯¯123)108¯−618¯−18 0¯
(g) 232÷2232÷2
Ans:
1162)232¯¯¯¯¯¯¯¯−23¯¯¯−2 12¯¯¯¯¯−120¯¯¯1162)232¯−23¯−2 12¯−120¯
(h)428÷2428÷2
Ans:
2242)428¯¯¯¯¯¯¯¯−42¯¯¯−2 8¯¯¯−80¯¯¯2242)428¯−42¯−2 8¯−80¯
21. Meera made 204 candles to sell in the market. She makes packets of 6. How many packets will she make? If she packs them in packets of 12, then how many packets will she make?
Ans: Number of candles made by Meera=204=204
Number of candles in each packet ==6=6
Total number of packets of candles =204÷6=34=204÷6=34
346)204¯¯¯¯¯¯¯¯−1824¯¯¯¯¯−240¯¯¯346)204¯−1824¯−240¯
Thus, 34 packets are required for 204 candles.
If Meera packs 12 candles in each packet then number of packets required for 204 candles
=204÷12=17=204÷12=17
1712)204¯¯¯¯¯¯¯¯−1284¯¯¯¯¯−840¯¯¯1712)204¯−1284¯−840¯
Thus, Meera will be needing 17 packets to pack 204 candles with each packet containing 12 candles.
22.On Sports Day, 161 children are in the school playground. They are standing in 7 equal rows. How many children are there in each row?
Ans: Students present in the playground=161=161
Number of rows=7=7
If the number of students are equal in each row then the number of students in each row
=161÷7=23=161÷7=23
237)161¯¯¯¯¯¯¯¯−1421¯¯¯¯¯−210¯¯¯237)161¯−1421¯−210¯
Thus, In each row there are 23 students.
23.

There are 8 packets of rakhis. Each packet has 6 rakhis in it. Your question:
Ans: Number of Rakhis in each packet =6=6
Total number of packets=8×6=46=8×6=46
Thus, there are a total of 46 rakhis in 8 packets.
My question: How many rakhis are there in total?
24.

There are 10 packets of sugar. Saurabh paid 110 rupees for all the packets. Your question:
Ans: Cost of 10 packets of sugar = Rs 110 =Rs110=��110
Cost of one packet of sugar =Rs110÷10=Rs11=��110÷10=��11
Thus,the cost of each packet of sugar is Rs 11.
What is the cost of 1 packet of sugar?
25.

There are 35 students in 7 rows. Each row has the same number of students. Your question:
Ans: Total number of students =35=35
Total number of row =7=7
If the number of students are equal in all the rows then each row has
=35÷7=7=35÷7=7students.
Thus, there are 7 students in each row.
How many students are there in each row?
26.Hari, Seema, Chinku and Lakshmi are going to Guwahati. The cost of one rail ticket is Rs 62.

Your question :
Ans: Cost of one ticket =Rs62=��62
Number of people =4=4
Total cost of the ticket =Rs62×4=Rs248=��62×4=��248
What is the total cost of the rail tickets?
27.One metre of cloth costs Rs 20. Lalbiak bought some cloth and paid Rs 140.

Ans: Total amount paid by Lalbiak=Rs140=��140
Cost of 1 metre of cloth =Rs20=��20
Total number of metres of cloth bought =Rs140÷20=Rs7=��140÷20=��7
Thus, Lalbaik bought 7 metres of clothes for Rs 140.
How many metres of cloth did Lalbiak buy?
NCERT Solutions for Class 4 Maths Chapter 11 Tables And Shares
If you want to arrange things in order then we can do it based on the concept of multiplication. Instead of repeating the addition of a number, we multiply the numbers. When we want to share something then we need to make equal parts that mean that we need to divide. Multiplication is the opposite of division.
Before we learn multiplication and division, we need to know the multiplication tables from 1 to 10.
We know the multiplication: 4 x 2 = 8. Here, 4 and 2 are called the factors of 8. 8 is called the multiple.
Let Us Understand Some Properties of Multiplication.
- When we multiply two numbers, the order of the numbers in which we multiply them does not matter. The product is the same. Ex: 9 x 7 = 63 or 7 x 9 = 63
- The product of a number when multiplied by 0 is 0.
Example: 8 x 0 = 0; 0 x 0 = 0
- The product of a number multiplied by 1 is always the number itself.
Example: 2 x 1 = 2; 1 x 2 = 2; 1 x 1 = 1
- When three numbers are multiplied, then the order of the numbers doesn’t matter. The result is always the same.
Example: 4 x 3 x 5 = 5 x 3 x 4
Division means repeated subtraction. If something is divided into equal groups, you can use a division method in order to find how many things are there in each group.
Example: If you have 12 sweets and you want to give 4 sweets to each friend. How many friends will get the sweets?
Solution:
There are 12 sweets.
Give four sweets to one friend. So you have 12 – 4 = 8 sweets left.
Give four sweets to another friend. You have 8 – 4 = 4 sweets left.
Give four sweets to another friend. You have 4 – 4 = 0 sweets left.
How many friends get the sweets? ______________.
Therefore, 12 put into equal groups of 4 each gives 3 groups
12 divided by 4 equals 3
12 ÷ 4 = 3
So what did we do in the above example? We repeatedly subtracted 4 from 12 till no sweets were left.
4 can be repeatedly subtracted from 12 three times.
The number to be divided is called a dividend. The number by which we divide is called the divisor. The result we get is called the quotient.
Properties of Division
- When we divide a number by 1 we get the same number as the quotient.
- When a number is divided by itself we get 1 as the quotient.
- When 0 is divided by any number we get 0.
Multiplication and Division
When we divide the multiple by one of the factors we get the other factor as the result.
Example: There are 3 boxes and 4 balls in each group.
(Image to be added soon) (Image to be added soon) (Image to be added soon)
Therefore, number of balls = 3 x 4 = 12
Multiplication means putting equal groups together.
Now, there are 12 balls.
(Image to be added soon)
Let us divide them into 3 equal groups.
(Image to be added soon) (Image to be added soon) (Image to be added soon)
There are 4 balls in each group.
Therefore, 12 ÷ 3 = 4
Division means splitting into equal groups
Hence, we see that multiplication and division are the opposite of each other.
We can also divide 12 balls into 4 groups of 3 each.
That is, 12 ÷ 4 = 3
Therefore, for one multiplication fact: 3 x 4 = 12
We can write two division facts: 12 ÷ 3 = 4 and 12 ÷ 4 = 3
Conclusion
These NCERT Solutions Maths Chapter 11 are provided for the convenience of students, so they can refer to the these solutions to clear any doubt regarding the sums of this chapter. Multiplication and division are the fundamental mathematical operations, and kids must learn these skills to excel in Mathematics.