Study Studio offers NCERT Solutions for Class 3 Maths Chapter 12 – Can We Share, designed by experienced teachers and subject experts as per the latest syllabus of CBSE Class 3. The NCERT Solutions for Class 3 Maths Chapter 12 PDF covers solutions for all the exercise questions given for this chapter in the NCERT textbook. Students can download these ‘NCERT Solutions Class 3 Maths Chapter 12- Can We Share?’ for free from Study Studio and go through them to secure good marks in the exam.
Access NCERT Solutions for Class 3 Mathematics Chapter 12 – Can We Share
1.

There are ________ caterpillars. They are in __________ groups. There are _________ caterpillars in each group.
Ans:
There are
2121
caterpillars. There are
33
groups. There are
77
caterpillars in each group.
2.

There are __________ laddoos. They are in ________ groups. There are _________ laddoos in each group.
Ans:
There are
1212
laddoos. They are in
44
groups. There are
33
laddoos in each group.
3. Draw
1818
stars. Put them into
22
equal group

There are _________ stars in each group.
Ans: The total number of stars are
1818
. To group it equally, divide
1818
by
22
. On dividing
1818
by
22
we get
99
.

There are
99
stars in each group.
4. Draw
1818
beads. Put them into 3 equal groups.

There are _________ beads in each group.
Ans: On dividing the
1818
by
33
, we get
66
There are
66
beads in each group.
5. Now draw the jalebis on the plates below, so that each plate has the same number of jalebis.
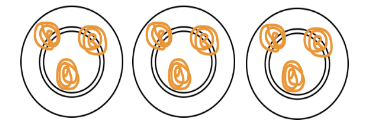
How many jalebis are there altogether? _________ How many jalebis are there in each plate? _________ Discuss in the class how you found the answer.
Ans:
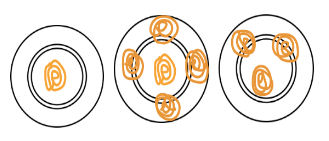
There are
99
jalebis all together. We have to distribute equally on
33
plates So we get
33
jalebis in each plate. Given the maximum number of jalebis in a plate is
55
. The Jalebi in second plate are more when compared to first and third plate. There are
55
jalebis in second plate so we need to remove
22
and transfer it in to first plate to make it as
33
jalebis and keep jalebis as it is in third plate because it’s already have
33
jalebis.
6. If there are
6060
bananas and two monkeys, how many will each monkey get? _________ bananas. What if there are
600600
bananas and two monkeys?
Ans: There are total
6060
bananas and two monkeys. If the monkeys divide the bananas equally then each monkey will get, on dividing
60÷2=3060÷2=30
.
Thus, each monkey will get
3030
bananas.
Suppose if there are
600600
bananas and it is to be divided among two monkeys then, the number of bananas each monkey will get, on dividing
600600
by
22
600÷2=300600÷2=300
Thus, each monkey will get
300300
bananas.
7. Five friends found
1010
five-rupee coins on the ground.

They shared them equally. Each friend got ten rupees.
50÷5=1050÷5=10
If there are
1616
ten-rupee notes and four friends to share, then
16÷4=416÷4=4
________ and
4×10=404×10=40
so each friend gets ________ rupees.
Five friends found Rs
100100
. If they share it equally, how much will each get? ________

Ans:
16÷4=416÷4=4
4×10=404×10=40
So, each friend gets
4040
rupees.
100÷5=20100÷5=20
So, each friend will get
2020
rupees.
8. Hari prashad has 30 meters of rope. He distributes it equally among his three children. Each child gets ___________ meters of rope. If there is 36 meters of rope, how much of rope will each child get? ___________ And if there is 60 meters of rope, how much will each child get? ___________

Ans:
- Given, Hari prashad has length of the rope =30=30meters
- Number of children getting the rope =3=3
- Length of the rope each child gets =30÷3=10=30÷3=10 meters.
- Therefore, each child will get 1010 meters of rope.
- If, Hari prashad has length of the rope =36=36meters
- Number of children getting the rope =3=3
- Length of the rope each child gets =36÷3=12=36÷3=12 meters.
- Therefore, if there is 3636 meters of rope, then each child will get 1212 meters of rope.
- If, Hari prashad has length of the rope =60=60meters
- Number of children getting the rope =3=3
- Length of the rope each child gets =60÷3=20=60÷3=20 meters.
- Therefore, if there is 6060 meters of rope, then each child will get 2020 meters of rope.
9. Minku puts her 15 laddoos equally into 5 boxes.
i) How many ladoos will there be in each box? There will be __________ laddoos in each box.
15÷5=15÷5=
_________
ii) If she uses only 3 boxes, how many laddoos will there be in each box? There will be __________ laddoos in each box. ________
÷3=÷3=
________
Ans:
i) Given, there are
1515
laddoos and
55
boxes are to be filled with these laddoos. So, number of laddoos in each box
=15÷5=3=15÷5=3
Hence, there will be
33
laddoos in each box.
ii) If she uses only
33
boxes.
Then, number of laddoos in each box
=15÷3=5=15÷3=5
Hence, there will be
55
laddoos in each box.
10. Share 25 bananas among 5 monkeys. How many bananas for each monkey?

______
÷5=÷5=
______ Each monkey has _________ bananas.
Ans:
We need to share 25 bananas for 5 monkeys
25÷5=525÷5=5
Hence, each monkey has
55
bananas.
11. Share 12 balloons among 3 boys. How many balloons for each boy?

_______
÷÷
_______
==
_______ Each boy has _________ balloons.
Ans:
We need to share 12 balloons among 3 boys.
12÷3=412÷3=4
Hence, each boy has
44
balloons.
12. There are 21 candles. Put them equally in 3 boxes. How many candles are there in each box?
Ans:
We need to put 21 candles are equally in 3 boxes.
Number of candles in each box
21÷3=721÷3=7
Hence, there are
77
candles in each box.
13. There are 18 socks. How many girls can wear these socks?

Ans:
Number of socks available
=18=18
Number of socks can each girl wear
=2=2
So, number of girls who can wear 18 socks
=18÷2=9=18÷2=9
Hence,
99
girls can wear 18 shocks.
14. Raj has 36 minutes to make rotis. One roti takes 3 minutes. How many rotis can he make in this time? He can make ____________ rotis.

Ans:
Raj has time to make rotis
=36=36
mins
Raj needs to prepare 1 roti
=3=3
mins
So, number of rotis can make in 36 mins
=36÷3=12=36÷3=12
Hence, Raj can make
1212
rotis in
3636
minutes.
15. These are 24 footmarks of goats. So how many goats were there?

Ans:
The number of foot a goat has
=4=4
Number of footmarks found in given figure
=24=24
Number of goats with 24 footmarks
=24÷4=6=24÷4=6
Hence, there were
66
goats.
16. Some girls are playing a game with both their hands. The girls who are playing have 60 fingers altogether. How many girls are playing this game?
Ans:
Number of fingers in the game (given figure)
=60=60
Number of fingers each girl has
=10=10
So, number girls having 60 fingers are
=60÷10=6=60÷10=6
Hence,
66
girls are playing a game with both their hands.
17. Lakshmi has 27 kg potatoes to sell. Three men came and bought equal amounts of potatoes. Each man bought __________ kg of potatoes.

Ans:
Number of potatoes Lakshmi has to sell
=27=27
kgs
If 27 kg of potatoes are equally bought by three men then each man will get
=27÷3=9=27÷3=9
kg
Hence, each man has taken
99
kg of potatoes.
18. Jumpy Animals.
 | A frog jumps 2 steps at a time. |
 | A squirrel jumps 3 steps. |
 | A rabbit jumps 5 steps. |
 | A horse jumps 15 steps. |
 | A kangaroo jumps 30 steps. |
19. Use the path on the next page to find out:
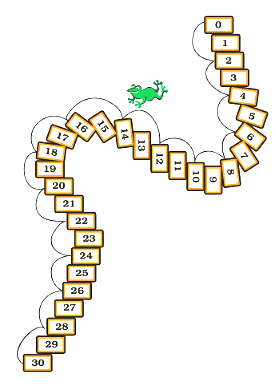
1. In how many jumps will the frog reach 30?
30÷2=30÷2=
_________
Ans:
30÷2=1530÷2=15
Frog will take 15 jumps to reach 30 steps.
2. In how many jumps will the squirrel reach 27?
27÷3=27÷3=
_________
Ans:
27÷3=927÷3=9
squirrel will take 9 jumps to reach 27 steps.
3. Which number will the kangaroo reach in two jumps?
Ans: we know that, Kangaroo takes 30 steps in one jump.
Thus, kangaroo will reach
=30×2=60=30×2=60
steps in two jumps.
4. Who all will meet at the number 15? _________, _________, _________
Ans: The number 15 comes in the table of 3, 5, and 15.
Squirrel will reach 15 steps because
=3×5=15=3×5=15
.
Rabbit will reach 15 steps because
=5×3=15=5×3=15
.
Horse will reach 15 steps because
=15×1=15=15×1=15
.
Hence, squirrel, rabbit, and horse will meet at number 15.
5. Will the rabbit ever be at the number 18? ________
Ans: Given, Rabbit’s one jump is equal to 5 steps
Thus, Rabbit can never be at 18 steps because 18 does not comes in the table of 5.
6. How many jumps of the rabbit equal one jump of the horse? ________
Ans:
A horse takes 15 steps in one jump.
A rabbit takes 5 steps in one jump.
15÷3=1515÷3=15
Hence, 3 jumps of the rabbit equal to one jump of the horse.
7. How many jumps of the horse equals two jumps of the kangaroo?
Ans:
A horse takes 15 steps in one jump.
2 jumps of the kangaroo
=2×30=60=2×30=60
steps.
60÷15=460÷15=4
Hence, 4 jumps of the horse equals two jumps of the kangaroo.
8. Which is the smallest number where the frog and the squirrel will meet?
Ans:
Frog’s takes two steps in one jump. So, frog takes steps 2, 4, 6, 8 and so on.
Squirrel’s takes three steps in one jump. So, frog takes steps 3, 6, 9, 12 and so on.
Number 6 is the common step of both frog and squirrel.
Thus, the smallest number where frog and squirrel will meet is 6th step.
20. Divide into groups of 2 using a 2 times table.
| 1818 | ÷÷ | 22 | == | 99 | Hint: 2×9=182×9=18 |
| 1818 | ÷÷ | == | 22 | ||
| 1616 | ÷÷ | 22 | == | ||
| 2020 | ÷÷ | 22 | == | ||
| ÷÷ | 22 | == | 77 | ||
| ÷÷ | 22 | == | 1010 | ||
| 88 | ÷÷ | == | 44 | ||
| ÷÷ | 22 | == | 55 |
Ans:
| 1818 | ÷÷ | 22 | == | 99 | Hint: 2×9=182×9=18 |
| 1818 | ÷÷ | 99 | == | 22 | Hint: 9×2=189×2=18 |
| 1616 | ÷÷ | 22 | == | 88 | Hint: 2×8=162×8=16 |
| 2020 | ÷÷ | 22 | == | 1010 | Hint: 2×10=202×10=20 |
| 1414 | ÷÷ | 22 | == | 77 | Hint: 2×7=142×7=14 |
| 2020 | ÷÷ | 22 | == | 1010 | Hint: 2×10=202×10=20 |
| 88 | ÷÷ | 22 | == | 44 | Hint: 2×4=82×4=8 |
| 1010 | ÷÷ | 22 | == | 55 | Hint: 2×5=102×5=10 |
21. Divide into groups of 5 using 5 times table.
| 1010 | ÷÷ | 55 | == | Hint: 5×2=?5×2=? | |
| 2020 | ÷÷ | == | 44 | ||
| 1515 | ÷÷ | 55 | == | ||
| 4040 | ÷÷ | == | 88 | ||
| 2020 | ÷÷ | 55 | == | ||
| ÷÷ | 55 | == | 66 | ||
| 2525 | ÷÷ | 55 | == | ||
| ÷÷ | 55 | == | 33 | ||
3535 | ÷÷ | 55 | == | ||
| ÷÷ | 55 | == | 22 |
Ans:
| 1010 | ÷÷ | 55 | == | 22 | Hint: 5×2=105×2=10 |
| 2020 | ÷÷ | 55 | == | 44 | Hint: 5×4=205×4=20 |
| 1515 | ÷÷ | 55 | == | 33 | Hint: 5×3=155×3=15 |
| 4040 | ÷÷ | 55 | == | 88 | Hint: 5×8=405×8=40 |
| 2020 | ÷÷ | 55 | == | 44 | Hint: 5×4=205×4=20 |
| 3030 | ÷÷ | 55 | == | 66 | Hint: 5×6=305×6=30 |
| 2525 | ÷÷ | 55 | == | 55 | Hint: 5×5=255×5=25 |
| 1515 | ÷÷ | 55 | == | 33 | Hint: 5×3=155×3=15 |
3535 | ÷÷ | 55 | == | 77 | Hint: 5×7=355×7=35 |
| 1010 | ÷÷ | 55 | == | 22 | Hint: 5×2=105×2=10 |
22. Try these.
| 44 | ÷÷ | == | 22 | ||
| 1414 | ÷÷ | 77 | == | ||
| 66 | ÷÷ | 33 | == | ||
| ÷÷ | 22 | == | 77 | ||
| ÷÷ | 22 | == | 33 | ||
| 1515 | ÷÷ | 33 | == | ||
| 88 | ÷÷ | 44 | == | ||
| 1515 | ÷÷ | 55 | == | ||
88 | ÷÷ | == | 44 | ||
| ÷÷ | 22 | == | 88 |
| 99 | ÷÷ | 33 | == | ||
| 1818 | ÷÷ | 99 | == | ||
| ÷÷ | 22 | == | 55 | ||
| 2020 | ÷÷ | 55 | == | ||
| 1212 | ÷÷ | 44 | == | ||
| 2020 | ÷÷ | 44 | == | ||
| 1212 | ÷÷ | == | 22 |
Ans:
| 44 | ÷÷ | 22 | == | 22 | Hint: 2×2=42×2=4 |
| 1414 | ÷÷ | 77 | == | 22 | Hint: 7×2=147×2=14 |
| 66 | ÷÷ | 33 | == | 22 | Hint: 3×2=63×2=6 |
| 1414 | ÷÷ | 22 | == | 77 | Hint: 2×7=142×7=14 |
| 66 | ÷÷ | 22 | == | 33 | Hint: 2×3=62×3=6 |
| 1515 | ÷÷ | 33 | == | 55 | Hint: 3×5=153×5=15 |
| 88 | ÷÷ | 44 | == | 22 | Hint: 4×2=84×2=8 |
| 1515 | ÷÷ | 55 | == | 33 | Hint: 5×3=155×3=15 |
88 | ÷÷ | 22 | == | 44 | Hint: 2×4=82×4=8 |
| 1616 | ÷÷ | 22 | == | 88 | Hint: 2×8=162×8=16 |
| 99 | ÷÷ | 33 | == | 33 | Hint: 3×3=93×3=9 |
| 1818 | ÷÷ | 99 | == | 22 | Hint: 9×2=189×2=18 |
| 1010 | ÷÷ | 22 | == | 55 | Hint: 2×5=102×5=10 |
| 2020 | ÷÷ | 55 | == | 44 | Hint: 5×4=205×4=20 |
| 1212 | ÷÷ | 44 | == | 33 | Hint: 4×3=124×3=12 |
| 2020 | ÷÷ | 44 | == | 55 | Hint: 4×5=204×5=20 |
| 1212 | ÷÷ | 66 | == | 22 | Hint: 6×2=126×2=12 |
NCERT Solutions for Class 3 Maths Chapter 12 Can We Share
As the name of Chapter 12– Can We Share suggests, this chapter is linked to division and distribution. This is a new concept. You can solve the sums given in the exercise and verify your answers with the NCERT Solutions for Class 3 Chapter 12 – Can We Share? to identify and correct your mistakes. You can go through these NCERT Solutions and prepare for your exams. You can also take the help of our experienced and friendly teachers if you have any doubts related to the topic.
NCERT Solutions for Class 3 Maths Chapter 12 – Can We Share? introduces the concept of division and distribution.
If we want to share something then we need to make equal parts. For example, your mother buys chocolate for you and she asks you to share with your sister. There are 8 pieces in the chocolate bar. How many does each get?
You and your sister get 4 pieces each. So, what are you doing here? You are making equal parts of the chocolate. This means splitting it into equal parts or groups or dividing it into equal parts.
Division means splitting or sharing into equal parts. The symbol of division is ‘ ÷ ‘.
Let us see an example.
(Image to be added soon)
In the above picture, there are 24 apples that need to be put equally in 6 boxes. How many apples will go into each box?
We have to distribute the apples in equal parts. So we write,
24 ÷ 6 = 4
The answer is 4 apples will go into each box. How did we get this answer? We have all 24 apples and we have divided the apples by the number of boxes.
The number to be divided is called the dividend. The number by which we divide the dividend is called the divisor. The result we get is called the quotient.
In the above example, 24 apples make the dividend. 6 boxes make the divisor, and the result, 4 apples is the quotient.
Why Do We Divide by Six Boxes?
We know the multiplication: 6 x 4 = 24. Here, 6 and 4 are called the factors of 24. 24 is called the multiple.
When we divide the multiple by one of the factors we get the other factor as the result. Hence you can say that division is opposite of multiplication.
Do we have to know tables to do division? Yes, you have to know the tables to do division. It will make our calculation faster.
Other Ways of Distribution
We can also distribute these 24 apples in other ways. We can divide the apples into 8 equal parts or 3 equal parts or 2 equal parts or 12 equal parts.
Let us see how many boxes we need in each kind of distribution.
- If we divide the apples into 8 equal parts then we need 3 boxes.
- If we divide the apples into 3 equal parts then we need 8 boxes.
- If we divide the apples into 12 equal parts then we need 2 boxes.
- If we divide the apples into 2 equal parts then we need _______ boxes? Can you guess?
The answer is 12 boxes.
Conclusion
With the help of this concept, now students can solve all the exercise questions given in the chapter and also verify them with the NCERT Solutions Maths Chapter 12. ‘Division’ is one of the fundamental mathematical operations. It is one of the basic skills that you need in your daily life. With the help of the concept of division, you can distribute time for all your daily activities, wisely. This concept will help when you will learn to count money as well.